
There have been a couple of comments or questions on the forum recently as regards accuracy at range, and rangefinding mechanisms, so I thought I had better give a quick rundown on how these things are done.
Though World of Tanks does model arc of fire, it assumes that you are an absolutely fantastic gunner who always knows exactly how far away the target is and applies superelevation accordingly. Superelevation is the amount of extra elevation that is applied to the gun above that on the direct line to the target, in order to account for the drop in flight due to gravity. Obviously at longer ranges, range estimation becomes both more critical, and more difficult. But if you want to hit your target, you have to figure out how far away it is, if you don’t want to just Kentucky-windage it. (Fire a round, see where it impacts, and adjust accordingly)
Here’s a case in point. One recent post on the forum referenced a comparison of the D-25-T 122mm gun with the 8.8L/71. The dispersion at long range for the two guns was more or less the same. This shouldn’t be too surprising, indeed, I wouldn’t be surprised to discover that today’s artillery cannon have lower dispersion rates than a tank cannon. (If you’re lobbing a round 30km with an expectation of it getting within fifty yards of where you’re aiming, despite being susceptible to weather effects for the 2 minute time of flight, you want a very good gun to begin with!).
Taking some –very- approximate numbers, assume about 780m/s for D-25-T. Assume a target a 1,500m. Absent the effect of air resistance (which is significant at that range) and extra distance due to the arc of flight, time of flight would be 1.92 seconds. For an 8.8cm/71 at about 1,000m/s time of flight is 1.5 seconds.
Now, let’s add a little variance. Let’s say the gunner eyeballed the distance at only 1,400m by visual observation which, face it, is a pretty good guess at nearly a mile. 1.79 seconds for 122mm, 1.4 seconds for 8.8cm. In the .13 of a second that the 122mm would take to get from the 1,400m aimpoint to the target at 1,500m, the effect of gravity (9.81m/s^2) would mean that the shell would effectively drop at least 2.36m (S=ut + ½(at^2), if my secondary school education is still good, subtract S where t = 1.86 from S where t=1.92). If aiming centre mass at a 2.7m high tank, pretty much a short round unless there’s a lucky dispersion. Again, excusing the crudity of the calculation, over the .1 of a second that the 8.8 round would take to cover the same distance, 1.4m would be the drop. There’s still a reasonable chance that the target would be hit.
In actuality at those ranges, the drop would be significantly more, as the round would be on the downward arc after reaching its maximum altitude (ordinate), and the round would have slowed down in its lateral movement due to the effect of wind resistance. If anyone happens to have the ballistic tables for these rounds, please feel free to chip in with the exact figures in the discussion.
This is one reason why guns which fire faster projectiles are generally considered to be more accurate, all other things being equal, as there is less time for gravity to affect the round and generate a miss: They are more forgiving of range and speed estimate errors.
Battlesight
As a general rule, tankers are taught to hit the target, and they don’t much care where. A 76mm punching through the TC’s cupola on a PzIV probably is going to be as significant an emotional event to the crew as the round going through the lower front hull. Only in particular cases did they aim at specific locations (such as the turret on Panther and not the front slope if the gun couldn’t punch through it), the default is ‘centre mass’. As a result, the most basic way of applying superelevation to gain a hit is what’s known today as a ‘battlesight’ range. Hunters may know the concept as “Maximum Point Blank”. This is the range that you aim at which the round will not arc so high as to fly over the target at any range at all, whilst still travelling as far as possible. On today’s M1A1, that range is 1,200m.
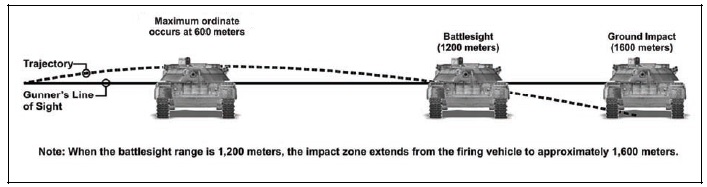
As you can see, though it takes about 600m for the round to drop half a target form, it’s only 400m before it drops the second half and impacts the ground, the effect of wind resistance over time. As a result, absent any other assistance, if the gunner aims at the target with the 1,200m graticle, he will hit it at all ranges from 0-1,600m. (We’ll discount the 30cm ground clearance). That’s with today’s velocity of some 1,680m/s though, granted, a smaller target than a Panther or IS-2. You can come to your own conclusions about the battlesight ranges for D-25-T or even the 8.8/71. (By way of comparison, M830 at 940m/s is 800m). Obviously the size of the target you’re shooting at is also a factor, the M1A1 assumes a T-72 variant.
For anything better than a battlesight engagement, you need a range input. There are all sorts of techniques for eyeballing a range to target, ideally you have been in position for a while and know how far various objects on the battlefield are and you can use them for reference. (Remember those range cards you had to fill out in Basic?). Count telephone poles. Flash-to-bang, if you have that many wits about you. Ideally, though, you want some form of assistance to make a more accurate estimate. They can either be part of the optic, or a separate complex rangefinder.
Mils
The ‘simplest’ (at least, for the perspective of the gunsight designer) is the mil reticle. If you ask someone how many mils are in a circle, you’ll probably get a different answer depending on who you talk to. NATO standard is 6,400. The mathematical answer is 2,000 x pi (about 6,283). More interesting, however, is that a mil is defined as the angle delineated by an object one unit in size when viewed at a distance of 1,000 units. So if you have an object 2 meters wide, and you look at it from 1,000m, it will be two mils wide on the scale. By having a system of determining size in mils in the gunsight, it is then possible to estimate with reasonable accuracy the range to target.
This is the reticle for Tiger.
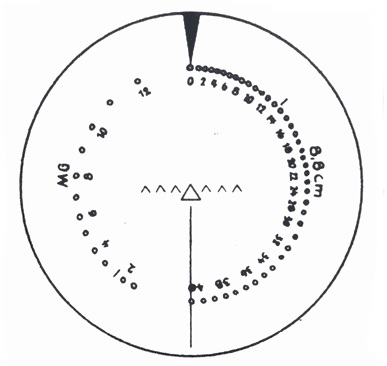
All those triangles in the middle are specifically sized. The big one is 4 mils wide, and 4 high (It’s not an equilateral triangle, if you’re curious). The smaller ones are 2 mils. Each triangle is spaced 2mils base to base, 4 mils point to point. From centre base to point of a small triangle is 1 mil. It’s 3 mils from the centre of one triangle to the base of the next one. And so on. This provides a lot of references to compare what you’re looking at against. Then all you have to do is know how many meters wide/high/long your target is (usually high, as it’s not aspect-dependant), and calculate accordingly.
Believe it or not, there’s actually an example of this technique used in Girls und Panzer, the fight against St Gloriana’s Academy. (For a cartoon, it’s very accurate).
This continues on today. If you look at the reticle of an M1 Abrams, the circle is 1 mil, the first horizontal line is 2 mils, the others 2.5 mils, they’re spaced 2 mils in height.
Choke
Now, if you’re not particularly good at mental arithmetic, your next bet is a choke sight. (There probably is an official name for it, but US tankers know it as ‘choke’)
These come in two formats. This one is from an M1.
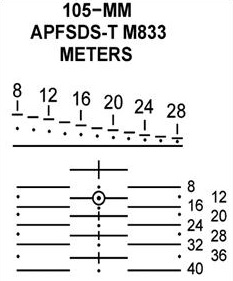
The graduation at the top is what you use to determine how far away your target is. Place the base of the vehicle on the level line, and move across until the roof matches with one of the various height lines. Whichever number is associated with that line, that’s how many hundreds of meters away the target is. Now, the downside is that the scale is graduated against a specific type of target, in this case, T-72. However, most Soviet tanks were more or less the same height, so it generally worked out.
If even this is too much work for you, the other variant is the funnel sight, which may also be familiar to modern fighter pilots. This one’s from a Bradley
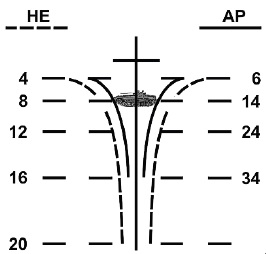
If you happen to have a perfect flank shot on a BMP in the Bradley, you don’t even need to estimate. The funnel is arced so that the apparent size of the target matches up with the two lines at exactly the right superelevation. Frontal targets require a slight aim-off, only from the vertical centre to the arc.
Known Angle
These are the first form of precision rangefinder, and they date back to naval use. If you look at many battleships, you’ll see little blisters on the edges of the turrets. They are the ports for rangefinder optics. Although ground-based versions did exist of similar size, more common were hand-held and vehicle mounted.

These work on the basis of known distance and known angle. Draw a right-angled triangle. The base of the triangle, maybe 1-2m long is the distance between the two lenses of the rangefinder. By adjusting the angle of one lens (i.e. the one not at 90 degrees), you can determine the angle at which line of sight of the two lenses intersect on the target. Doing some simple trigonometry, you can then work out the length of the long side of the triangle, which is the range to target.
These basically come in two categories, Stereoscopic and Coincidence.

Stereoscopic rangefinders were the type used by the US military on its tanks by the end of WWII. They work on the basis of the brain's ability to merge the two images from the two eyeballs into one. A mark would be visible in each eyepiece. The idea was for the two marks to become merged into one final mark (or V-shaped pattern, in the US systems) on the target. Supposedly pretty good in theory, but the US found that most troops simply did not have the visual actuity to make the most of the system.

Coincidence rangefinders such as on Conqueror and later US tanks work on a similar idea, and again, you’ll probably be familiar from other computer games, particularly submarine ones. Take one image, and split it into two halves, usually top and bottom. One lens shows the top of half of the image, the other lens the bottom half. They are misaligned. Move the bottom half to merge with the top half (or whatever), and the angle that results gives you the range.
Reflection

This all still was pretty complicated, and there was some simplification to come for the users, happily. One of the earlier attempts was OPTAR, Optical Tracking, Acquisition and Ranging, you’ll see it on the side of your T110E5 model. (Or on the T95 above). Basically it works on the basis of reflected light. Flash, time the return. Things became a little bit more refined with the advent of the laser rangefinder of today, which is accurate to a ridiculously over-necessary level (As long as you use it correctly, you’ll be surprised how many people don’t know how to correctly use first or last return).
And so that brings us up to today, and how to determine range in your tank. Knowing how far away, of course, is only part of the problem, but that’s another article.
The Chieftain is Wargaming America's resident tank guru. If you'd like to stay abreast of his comings and goings, feel free to "Like" The Chieftain on Facebook and follow The Chieftain on Twitter.